
During the summer, UCLA offers compelling courses that welcome the curious to connect with the physical sciences. Whether you are a high school student, a college student, a working professional, or a lifelong learner, we invite you to study in an environment that appreciates diversity and global perspectives.
Whether you are trying to get into that impacted course you couldn’t during the academic year, exploring your career options, completing those last few courses to graduate, or even taking your first college course as a high school student, UCLA Summer Sessions is here to help you with the next step in your academic career.
Join the tens of thousands of students who say that UCLA Summer Sessions is an invigorating and unforgettable experience academically, culturally, and socially. You will have an experience that will challenge and inspire you.
Dozens of unique courses in each of the six Physical Sciences departments are offered during the summer in two sessions, Session A and Session C. If you have questions, please don’t hesitate to email physicalscience@ucla.edu.
All courses will be offered via remote learning. For information about enrollment, fees, deadlines, and more visit UCLA Summer Sessions website.
Courses Being Offered
Atmospheric & Oceanic Sciences
Session A:
- 1 – Climate Change: From Puzzles to Policy
- 2 – Air Pollution
- M105 – Introduction to Chemical Oceanography
Session C:
- 1 – Climate Change: From Puzzles to Policy
Both 1 and 2 have the option for lab credit. High school students are welcome in 1 or 2. 105 is an upper division course.
For information about enrollment, fees, deadlines, and more visit UCLA Summer Sessions website.
Chemistry & Biochemistry
Exciting new general electives include 101 – Catalysis in Modern Drug Discovery.
Other online courses include:
- 14A. General Chemistry for Life Scientists I
- 14B. General Chemistry for Life Scientists II
- 14BL. General and Organic Chemistry Laboratory I
- 14C. Structure of Organic Molecules
- 14CL. General and Organic Chemistry Laboratory II
- 17. Chemical Principles
- 20A. Chemical Structure
- 20B. Chemical Energetics and Change
- 30A. Organic Chemistry I: Structure and Reactivity
- 30B. Organic Chemistry II: Reactivity, Synthesis, and Spectroscopy
- 153A. Biochemistry: Introduction to Structure, Enzymes, and Metabolism
- 153B. Biochemistry: DNA, RNA, and Protein Synthesis
- 153L. Biochemical Methods I
Online Chemistry and Biochemistry courses
Three-week summer intensive courses are also offered to UCLA students with some prerequisites.
For information about enrollment, fees, deadlines, and more visit UCLA Summer Sessions website.
Earth, Planetary, and Space Sciences
EPSS 1
The course introduces the elements of Earth science, including study of Earth materials and the nature and interpretation of geologic evidence; study of geologic processes and historical aspects of geology are also covered. After this course, the students will better be able to describe and understand the main geological processes ruling our Earth’s system.
EPSS M7
Space weather is an emerging domain of the space sciences includes the study of conditions in space that impact society its technological systems. Space weather occurs as a consequence of the dynamic behavior of the sun, and its interaction with the Earth’s magnetic field and atmosphere. This class is an introduction to space weather suitable for all majors. The phenomenology of the solar-terrestrial relationship will be introduced and basic physics describing the interaction will be explored. The goal of the course will be to have students understand the physical processes that connect the variable sun to the Earth through an exploration of the societal impacts of Space Weather
EPSS9
This class will cover the entire solar system, from the rocky planets to the gas and ice giants, the comets, the asteroids, the satellites and rings, the Centaurs, Kuiper belt objects and Oort cloud, and we will go beyond to consider the planetary systems of other stars and the likelihood and distribution of life.
EPSS 15
A comprehensive introduction to our largest environment on Earth: The Ocean. This course will provide a basic understanding of plate tectonics, ocean currents and waves, seawater chemistry, marine food webs, biological processes, and impacts of climate change.
EPSS 16
By considering life on Earth from a Cosmic perspective, and using as its prime exemplar the interconnected evolutionary histories of our planet’s geology, biology, and its atmosphere-ocean system, this course seeks to break down the traditional fragmented view of the natural world. In doing so, the course will (1) explore topics drawn from diverse academic disciplines — in the Physical Sciences, from Physics & Astronomy, Chemistry & Biochemistry, Earth, Planetary & Space Sciences, and Atmospheric and Oceanic Science; and in the Life Sciences, from Cell & Molecular Biology, Microbiology & Molecular Genetics, and Organismal & Evolutionary Biology; (2) use historical (1700s) and fairly recent vignettes (e.g., NASA’s 1996 announcement of “evidence of fossil life on Mars”) to illustrate the humanness of scientists and how science actually is done; and (3) introduce knowledge and concepts that should be of lasting value to an educated citizen.
Mathematics
Please note: All courses are open to qualified high school students. 3A, 3B, 31A, 31B cover AP Calculus content at university level, while 32A, 32B, 33A, 33B cover more advanced content suitable only for students who have already completed the prerequisite course stated in the course description, or its equivalent.
MATH 1 – Precalculus
Lecture, three hours; discussion, one hour. Preparation: three years of high school mathematics. Requisite: successful completion of Mathematics Diagnostic Test. Function concept. Linear and polynomial functions and their graphs, applications to optimization. Inverse, exponential, and logarithmic functions. Trigonometric functions.
MATH 3C – Ordinary Differential Equations with Linear Algebra for Life Sciences Students
Lecture, three hours; discussion, one hour. Requisite: course 3B with grade of C- or better. Multivariable modeling, matrices and vectors, eigenvalues and eigenvectors, linear and nonlinear systems of differential equations, probabilistic applications of integration.
COMPTNG 10A – Introduction to Programming
Lecture, three hours; discussion, two hours; laboratory, eight hours. No prior programming experience assumed. Basic principles of programming, using C++; algorithmic, procedural problem solving; program design and development; basic data types, control structures and functions; functional arrays and pointers; introduction to classes for programmer-defined data types.
MATH 31A – Differential and Integral Calculus
Lecture, three hours; discussion, one hour. Preparation: at least three- and one-half years of high school mathematics (including some coordinate geometry and trigonometry). Requisite: successful completion of Mathematics Diagnostic Test or course 1 with grade of C- or better. Differential calculus and applications; introduction to integration.
MATH 31B – Integration and Infinite Series
Lecture, three hours; discussion, one hour. Requisite: course 31A with grade of C- or better. Not open for credit to students with credit for course 3B. Transcendental functions; methods and applications of integration; sequences and series.
MATH 32A – Calculus of Several Variables
Lecture, three hours; discussion, one hour. Enforced requisite: course 31A with grade of C- or better. Introduction to differential calculus of several variables, vector field theory.
MATH 32B – Calculus of Several Variables
Lecture, three hours; discussion, one hour. Enforced requisites: courses 31B and 32A, with grades of C- or better. Introduction to integral calculus of several variables, line and surface integrals.
MATH 33A – Linear Algebra and Applications
Lecture, three hours; discussion, one hour. Enforced requisite: course 3B or 31B or 32A with grade of C- or better. Introduction to linear algebra: systems of linear equations, matrix algebra, linear independence, subspaces, bases and dimension, orthogonality, least-squares methods, determinants, eigenvalues and eigenvectors, matrix diagonalization, and symmetric matrices.
MATH 33B – Differential Equations
Lecture, three hours; discussion, one hour. Enforced requisite: course 31B with grade of C- or better. Highly recommended: course 33A. First-order, linear differential equations; second-order, linear differential equations with constant coefficients; power series solutions; linear systems.
MATH 61 – Introduction to Discrete Structures
Lecture, three hours; discussion, one hour. Requisites: courses 31A, 31B. Not open for credit to students with credit for course 180 or 184. Discrete structures commonly used in computer science and mathematics, including sets and relations, permutations and combinations, graphs and trees, induction.
MATH 95 – Transition to Upper-Division Mathematics
Lecture, three hours; discussion, one hour. Enforced requisites: courses 32A, 32B. Not open for credit to students with credit for course 131A or 132. Introduction to rigorous methods of proof-based upper-division mathematics courses. Basic logic; structure of mathematical proofs; sets, functions, and cardinality; natural numbers and induction; construction of real numbers; topology of real numbers; sequences and convergence; continuity. May not be applied toward major requirements.
MATH 110A – Algebra
Lecture, three hours; discussion, one hour. Requisite: course 115A. Not open for credit to students with credit for course 117. Ring of integers, integral domains, fields, polynomial domains, unique factorization.
MATH 115A&C – Linear Algebra
Lecture, three hours; discussion, two hours. Requisite: course 33A. Techniques of proof, abstract vector spaces, linear transformations, and matrices; determinants; inner product spaces; eigenvector theory.
MATH 131A&C – Analysis
Lecture, three hours; discussion, one hour. Requisites: courses 32B, 33B. Recommended: course 115A. Rigorous introduction to foundations of real analysis; real numbers, point set topology in Euclidean space, functions, continuity.
MATH 132 – Complex Analysis for Applications
Lecture, three hours; discussion, one hour. Requisites: courses 32B, 33B. Introduction to basic formulas and calculation procedures of complex analysis of one variable relevant to applications. Topics include Cauchy/Riemann equations, Cauchy integral formula, power series expansion, contour integrals, residue calculus.
MATH 134 – Linear and Nonlinear Systems of Differential Equations
Lecture, three hours; discussion, one hour. Requisite: course 33B. Dynamical systems analysis of nonlinear systems of differential equations. One- and two- dimensional flows. Fixed points, limit cycles, and stability analysis. Bifurcations and normal forms. Elementary geometrical and topological results. Applications to problems in biology, chemistry, physics, and other fields.
MATH 135 – Ordinary Differential Equations
Lecture, three hours; discussion, one hour. Requisites: courses 33A, 33B. Selected topics in differential equations. Laplace transforms, existence and uniqueness theorems, Fourier series, separation of variable solutions to partial differential equations, Sturm/Liouville theory, calculus of variations, two-point boundary value problems, Green’s functions.
MATH 142 – Mathematical Modeling
Lecture, three hours; discussion, one hour. Requisites: courses 32B, 33B. Introduction to fundamental principles and spirit of applied mathematics. Emphasis on manner in which mathematical models are constructed for physical problems. Illustrations from many fields of endeavor, such as physical sciences, biology, economics, and traffic dynamics.
MATH 151A – Applied Numerical Methods
Lecture, three hours; discussion, one hour. Requisites: courses 32B, 33B, 115A, Program in Computing 10A or Computer Science 31. Introduction to numerical methods with emphasis on algorithms, analysis of algorithms, and computer implementation issues. Solution of nonlinear equations. Numerical differentiation, integration, and interpolation. Direct methods for solving linear systems.
MATH 151B – Applied Numerical Methods
Lecture, three hours; discussion, one hour. Requisite: course 151A. Introduction to numerical methods with emphasis on algorithms, analysis of algorithms, and computer implementation issues. Solution of nonlinear equations. Numerical differentiation, integration, and interpolation. Direct methods for solving linear systems.
MATH 156 – Machine Learning
Lecture, three hours; discussion, one hour. Requisites: courses 115A, 164, 170A or 170E or Statistics 100A, and Computer Science 31 or Program in Computing 10A. Strongly recommended requisite: Program in Computing 16A or Statistics 21. Introductory course on mathematical models for pattern recognition and machine learning. Topics include parametric and nonparametric probability distributions, curse of dimensionality, correlation analysis and dimensionality reduction, and concepts of decision theory. Advanced machine learning and pattern recognition problems, including data classification and clustering, regression, kernel methods, artificial neural networks, hidden Markov models, and Markov random fields. Projects in MATLAB to be part of final project presented in class.
MATH 164 – Optimization
Lecture, three hours; discussion, one hour. Enforced requisites: courses 115A, 131A. Not open for credit to students with credit for former Electrical Engineering 136. Fundamentals of optimization. Linear programming: basic solutions, simplex method, duality theory. Unconstrained optimization, Newton method for minimization. Nonlinear programming, optimality conditions for constrained problems. Additional topics from linear and nonlinear programming.
MATH 167 – Mathematical Game Theory
Lecture, three hours; discussion, one hour. Requisite: course 115A. Quantitative modeling of strategic interaction. Topics include extensive and normal form games, background probability, lotteries, mixed strategies, pure and mixed Nash equilibria and refinements, bargaining; emphasis on economic examples. Optional topics include repeated games and evolutionary game theory.
MATH 170E – Introduction to Probability and Statistics 1: Probability
Lecture, three hours; discussion, one hour. Requisites: courses 31A, 31B. Not open to students with credit for course 170A, Electrical and Computer Engineering 131A, or Statistics 100A. Introduction to probability theory with emphasis on topics relevant to applications. Topics include discrete (binomial, Poisson, etc.) and continuous (exponential, gamma, chi-square, normal) distributions, bivariate distributions, distributions of functions of random variables (including moment generating functions and central limit theorem).
MATH 170S – Introduction to Probability and Statistics 2: Statistics
Lecture, three hours; discussion, one hour. Requisites: courses 31A, 31B, and 170A or 170E. Not open to students with credit for Statistics 100B. Introduction to statistics. Topics include sampling, estimation (maximum likelihood and Bayesian), properties of estimators, regression, confidence intervals, hypotheses testing, analysis of variance.
MATH 174E – Mathematics of Finance for Mathematics/Economics Students
Lecture, three hours; discussion, one hour. Enforced requisites: courses 33A, and 170A or 170E or Statistics 100A. Not open for credit to students with credit for course 174A, Economics 141, or Statistics C183/C283. Mathematical modeling of financial securities in discrete and continuous time. Forwards, futures, hedging, swaps, uses and pricing (tree models and Black-Scholes) of European and American options, Greeks and numerical methods.
MATH 177 – Theory of Interest and Applications
Lecture, three hours; discussion, one hour. Requisite: course 32B. Types of interest, time value of money, annuities and similar contracts, loans, bonds, portfolios and general cash flows, rate of return, term structure of interest rates, duration, convexity and immunization, interest rate swaps, financial derivatives, forwards, futures, and options.
MATH 182 – Algorithms
Lecture, three hours; discussion, one hour. Requisite: course 3C or 32A, and 61. Not open for credit to students with credit for Computer Science 180. Graphs, greedy algorithms, divide and conquer algorithms, dynamic programming, network flow. Emphasis on designing efficient algorithms useful in diverse areas such as bioinformatics and allocation of resources.

Physics & Astronomy
PHYS 10: Physics
This is a general introductory course intended for anyone that wants not only a broad overview, but real understanding of the basic elements of physics discovered over the last 400 years. Special mathematical preparation beyond that necessary for admission to University in freshman standing is not required.

Course topics include planetary motion, Newton’s laws, universal gravitation, electricity and magnetism, wave motion, light, sound, heat, relativity, quantum mechanics, atoms, and subatomic particles. The approach will be quantitative with conceptual ideas treated seriously. As time permits, development of physical ideas will be placed in their cultural and historical perspectives.
ASTR 5: Life In the Universe
This introductory class takes a scientific approach to the greatest question of humanity: “Are we alone?” The course begins with life on Earth and investigates the serious prospect of finding life elsewhere in the Universe.
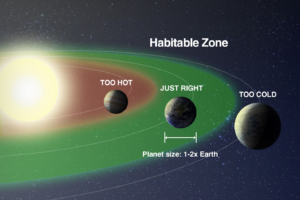
The discovery of planets and moons around other stars discovered in the last two decades offers this tantalizing hope of finding life in other planetary systems. The course will teach the necessary fundamentals of astronomy and biology in addition to some chemistry, geology, and physics for understanding simple and complex life. Selected topics are treated in some depth, but little or no formal mathematics is required.
Statistics
Session C